Entdecken Sie das neueste Rätsel in unserer Geometrie-Reihe
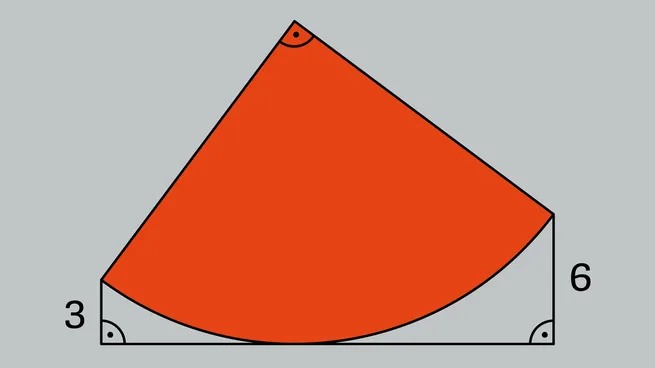
Berechnen Sie die Fläche eines Viertelkreises, der leicht nach links geneigt ist und mit seiner runden Seite eine Tangente berührt. Gegeben sind die senkrechten Abstände der Ecken zur Tangente, die 3 und 6 betragen.
Mit dem Satz des Pythagoras ermitteln wir den Radius r des Viertelkreises, der sich als 15 herausstellt. Daraus erhalten wir eine Fläche von π*225/4, was etwa 176,7 entspricht.
Dieses Rätsel wurde in der Facebook-Gruppe „Geometria Super Top“ entdeckt.
Haben Sie frühere Rätsel verpasst?
- Sechsstellige Zahl gesucht
- Welche Ziffer fehlt?
Tauchen Sie ein in die faszinierende Welt der Geometrie!
Für mehr Informationen lesen Sie auf spiegel


















Diskussion darüber post